Mars’s induced magnetosphere can degenerate

Introduction

Unmagnetized bodies with sufficiently dense ionospheres, such as Mars and Venus, can be considered as conductors immersed in the moving solar wind plasma with velocity V₀ carrying the frozen-in IMF B₀. In the frame of reference of the conductor, the electromagnetic field comprises two components: B₀ and the convective electric field E = −V₀ × B₀. The convective field results in a potential difference across the conductor, which, in turn, results in induction currents flowing through the conductor (unipolar induction). The magnetic fields associated with the induction currents cancel (or reduce because of finite conductivity) the magnetic field inside the ionosphere (Lenz’s law). Above the ionosphere, the induced fields act on the solar wind plasma by deviating it. Thus, a void called an induced magnetosphere is created. The magnetic pressure of the induced fields balances the dynamical and thermal pressures of the hot magnetosheath plasma. Under nominal conditions, the Parker angle at Mars is about 57° (ref. ²), and the mechanism above operates. However, in some rare cases, the cone angle, which is the angle between the solar wind velocity and the IMF, can be very low, below about 10°. For example, this occurred during approximately 2% of all MAVEN orbits from 2014 to 2019. In this case, the convective electric field responsible for generating the induction currents weakens, or, in other words, the magnetic flux through the conductive ionosphere responsible for the electromotive force significantly reduces, so that the mechanism described above does not operate any more. When the interaction of unmagnetized bodies with the solar wind occurs for very small cone angles so that the convective electric field is very weak, we say that the induced magnetosphere is degenerate. Dubinin et al.³ noted this very peculiar case for the interaction at Venus and also identified the interaction as a degenerate, induced magnetosphere. This type of interaction has recently attracted attention^11,12,13. We use the term degenerate, induced magnetosphere to emphasize the fundamental difference in the structure and physics of such interaction.

Earlier studies of the solar wind’s interaction with Venus for small cone angles, which utilized Pioneer Venus Orbiter measurements, focused on magnetosheath turbulence and wave–particle interactions that resulted in planetary-ion pickup¹⁴. The structure and morphology of the interaction region have received less attention. In general, the electrodynamics of degenerate magnetospheres are not well understood, and the question is open as to what, if anything, serves as a solar wind obstacle. From measurements at Mars and Venus, it is still not clear whether or not a magnetosphere-like void or, in other words, a magnetic barrier, forms for very small cone angles.

De Zeeuw et al.¹⁵ used a two-dimensional magnetohydrodynamics model to simulate the interaction between the solar wind and Venus during a radial IMF and found that a magnetotail was not induced. Using data from the magnetometer onboard Venus Express, Zhang et al.¹¹ conducted a case study in which the cone angle was 11° and noted the absence of a solar wind void, referred to as a ‘magnetic barrier’ in their terminology. Dubinin et al.³ analysed combined magnetic field and particle data from Venus Express and highlighted that ‘spatially varying IMF across the planet will produce a magnetic field which looks like the field of a degenerated dipole with its axis aligned with the solar wind flow’ so that a magnetic barrier forms. Chang et al.¹² performed a statistical study of all available Venus Express data and identified 13 cases when the cone angle was below 20°. Those authors emphasized the role of the magnetic field tension ((B ⋅ ∇)B/μ₀) in deviating the solar wind plasma. This tension contributed to the existence of a ‘weak’ magnetic barrier that could balance the solar wind’s dynamical pressure, although it is not clear how, as this term was very small. Fowler et al.¹³ analysed in detail low-altitude observations (down to 250 km) of the solar wind at small solar zenith angles (20°–30°) made by the MAVEN spacecraft. They concluded that this case corresponds to a small cone angle, although MAVEN, being in a low-altitude orbit, did not reach the undisturbed solar wind. A pressure balance analysis indicated that the magnetic pressure in the region matched the estimated upstream dynamic pressure of the solar wind. Fowler et al.¹³ suggested that a magnetic barrier formed in the deep ionosphere.

Pioneer Venus Orbiter observed a quasi-parallel bow shock at Venus, which extended to high solar zenith angles, resulting in intense turbulence, wave–particle interactions and heating of planetary ions on the dayside¹⁰. Fowler et al.¹³ reported similar heating at Mars. Ions propagate upstream along parallel magnetic field lines, resulting in erosion of the ionospheric density, as seen in hybrid simulations of Venus by Omidi et al.¹⁶. Masunaga et al.¹⁷ claimed that the total escape rate does not depend on the cone angle, but their focus was solely on the downtail target area.

Degenerate, induced magnetospheres are open systems, meaning that the solar wind can reach the ionosphere or even the collisional boundary¹³. This enables the transfer of energy, associated with both waves and direct kinetic energy of the solar wind particles, from the upstream region to the ionosphere, which could be another ionization source¹⁸. All these features make a degenerate, induced magnetosphere a distinctive mode of solar wind interactions that warrants dedicated detailed studies. Degenerate, induced magnetospheres are also common for unmagnetized exoplanets close to their parent stars, where the magnetic field tends to be nearly parallel to the stellar wind.

Observations by MAVEN and MEX

This study is based on simultaneous observations (Extended Data Fig. 1) by MAVEN (Extended Data Fig. 2) and MEX (Extended Data Fig. 3) from 07:00 to 09:40 utc on 2 July 2018. We utilized measurements made by the solar wind ion analyser¹⁹, the solar wind electron analyser²⁰, the suprathermal and thermal ion composition instrument²¹ and the magnetometer²² onboard MAVEN. We also used measurements made by the ion mass analyser⁵ and the electron spectrometer⁵ onboard MEX. The cone angle was 4° as calculated from the solar wind ion analyser and magnetometer data in the undisturbed solar wind (Extended Data Fig. 2h). The other upstream parameters, detailed in Extended Data Table 1, are typical for Mars. The upstream parameters in the table were computed by averaging MAVEN observations over time from 07:00 to 07:45 when the spacecraft was in the undisturbed solar wind, as can be seen in Extended Data Fig. 2. The cone angle of 4° that we got from the averaged magnetic field and velocity values is smaller than the cone angle of 7° averaged from the instantaneous values. This ambiguity was unavoidable, as we had to pick only one set of upstream conditions to represent the observed time-variable upstream conditions for our simulations. We chose only the inbound part of the orbits for this study because the solar wind conditions could have changed while the spacecraft was inside the interaction region. MAVEN collected data from upstream at the terminator. It had an apoapsis altitude of approximately 6,100 km to the terminator’s ionosphere and reached a periapsis altitude of approximately 165 km (Extended Data Fig. 1). MEX sampled from further upstream on the dayside, with an apoapsis altitude of approximately 10,000 km. It extended deeper into the magnetotail and reached a periapsis altitude of approximately 370 km (Extended Data Fig. 1).

MAVEN’s measurements relevant for the analysis start from the undisturbed solar wind. At 07:45, the spacecraft entered the foreshock region, a disturbed region upstream of a shock-like boundary (see more discussion below). This region was identified by the strong fluctuations in the magnetic field (Extended Data Fig. 2f,g) and the extra populations of ions with an energy higher than the solar wind energy (Extended Data Fig. 2a). The latter were planetary ions and visible in Extended Data Fig. 2c, but note that the solar wind ion analyser does not resolve masses. These ions were at considerable distances from the shock crossing at 08:11 (Extended Data Fig. 2c,e). By applying the magnetic coplanarity theorem²³, we obtained a shock normal angle of 46°. Thus, the shock, if it is indeed a shock, was quasi-perpendicular, as expected, in the flank. It was probably a weak shock, as revealed by the insignificant proton and electron heating, and the Mach number barely changed on passing through this weak shock (from 8 to 7), but the exact nature of such shocks for degenerate, induced magnetospheres requires further investigation. Hence, we refer to it as a flank shock in this paper, although no clear induced-magnetosphere boundary has been identified, because there was no sharp enhancement of the magnetic field accompanied by an increase of planetary ions and cold electrons. If the shock is confirmed in future studies, the nature of the obstacle creating it is a puzzle. During the period 07:45–08:50, MAVEN was moving through a structure specific for degenerate, induced magnetospheres, a cross-flow plume of heavy ions, which overlapped with the magnetosheath-like region identified by the weakly heated protons. The magnetic field exhibited strong fluctuations, a factor of four in magnitude, that could also be important for understanding the physics of the flank shock. The exact nature of this domain is not clear either, as the conventional features of an induced magnetosphere and bow shock were not observed. From 08:50 to 9:30, the heavy-ion fluxes slowly decreased. At 09:30, MAVEN entered the ionosphere, as was identified by the presence of a low-energy planetary-ion population. The solar wind persisted until it reached the ionosphere (Extended Data Fig. 2d). For comparison with simulations, we also present macroscopic parameters obtained by integrating the measured differential fluxes, the proton and \({{\rm{O}}}_{2}^{+}\) densities, as well as the magnetic field.

Extended Data Fig. 3 shows observations from MEX, including the energy spectra and densities of protons, heavy ions and electrons. Like MAVEN, MEX also captured features of a strong foreshock between 07:50 and 08:20 (Extended Data Fig. 3b), high fluxes of heavy ions in the sheath region (Extended Data Fig. 3c) and no typical signatures of a crossing of the induced-magnetosphere boundary. The proton, heavy-ion and electron densities in Extended Data Fig. 3d–f were derived by integrating the respective differential fluxes. Although there was reasonable agreement between the proton and electron densities (the heavy ions contributed very little) when MEX was in the solar wind, the densities were significantly different from 08:26 to 08:42. This interval corresponds to when MEX crossed the flank shock and entered the magnetosheath-like structure. The discrepancy could be attributed to the shock being weak. As MEX passed through this weak shock, the solar wind maintained its supersonic speed but underwent a directional change and became partially obscured by the spacecraft structure, owing to how the ion mass analyser was installed on MEX. As the shock was weak, there was no substantial heating. The ion mass analyser covered only a fraction of the distribution function, leading to an underestimation of the proton density. The electron density measurements, however, are reliable because of the broader electron distribution function.

The dashed lines in Extended Data Figs. 2 and 3 represent the results from the hybrid model, which were compared with observations.

Hybrid simulations

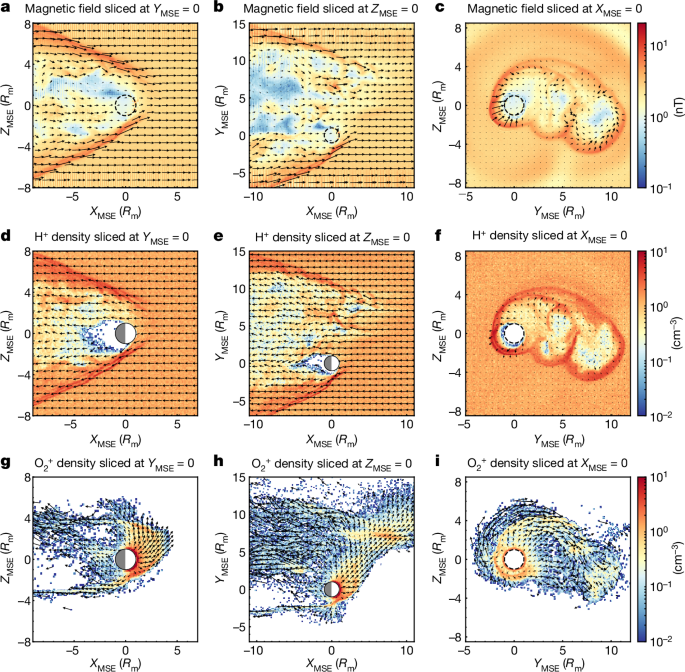
Using the observed upstream parameters from MAVEN (Extended Data Table 1), we performed a hybrid simulation of the relevant interaction. The model is described in more detail in Zhang et al.^24,25, Holmstrom²⁶ and references therein. In the model, electrons are treated as an inertialess charge-neutralizing fluid, whereas ions are treated as particles (grouped together as macroparticles). The ion motion is determined by the fields obtained from a generalized Ohm’s law. The model incorporates two solar wind species (H⁺ and He⁺⁺) and three planetary species (\({{\rm{O}}}^{+},{{\rm{O}}}_{2}^{+}\) and \({{\rm{CO}}}_{2}^{+}\)). The ionosphere is represented by the upflux of ionospheric ions from its inner boundary. The heavy ions are produced on the dayside from the obstacle boundary, with an initial velocity drawn from a Maxwellian distribution corresponding to a temperature of 200 K. The ion upflux decays from the subsolar point to the terminator by the cosine of the solar zenith angle. The ion upflux is a free parameter in our model.

We used MAVEN’s upstream observations as input in the model. We ran different simulations with different ion upfluxes. We thereafter chose the run that best matched the observations. The total ion upflux we used was 4.8 × 10²⁵ s^−1. The model was configured in the MSE frame, with the the x axis antiparallel to the solar wind velocity, the z axis aligned with the solar wind convective electric field −V × B and the y axis completing the right-handed coordinate system. The magnetic field was stored on a uniform grid with a spatial resolution of 350 km. The inner boundary was set at 170 km altitude above Mars, approximately corresponding to the exobase altitude. Ions inside the inner boundary were removed from the simulation. We solved a magnetic diffusion equation inside the inner boundary. Crustal fields were not included in the model.

Extended Data Fig. 4 illustrates that the convective electric field predominated at high altitudes, whereas the ambipolar field was dominant near the planet, at altitudes of several hundreds of kilometres.

Comparison of the simulations and measurements

The model results are compared both to MAVEN and MEX measurements made along their trajectories (dashed lines in Extended Data Figs. 2d–g and 3d–h). An overview of the proton density and \({{\rm{O}}}_{2}^{+}\) density distributions in their orbit planes is shown in Extended Data Figs. 2j–k and 3j–k. In general, the simulation and measurements are in good agreement.

MAVEN’s orbit was almost in the terminator plane. The agreement can be seen in the proton density (Extended Data Fig. 2d) and magnetic field (Extended Data Fig. 2g). At 7:45, the oscillations of the magnetic field increased in the foreshock region, coinciding with the observations of planetary ions. Around 8:11, an abrupt rise in the magnetic field magnitude and proton density indicates a flank shock crossing, which is evident in the model as well (Extended Data Fig. 2d,j). The prominent \({{\rm{O}}}_{2}^{+}\) flux from 7:45 to 8:50, visible in Extended Data Fig. 2k, indicates the presence of planetary ions in the magnetosheath-like structure. The delayed increase in \({{\rm{O}}}_{2}^{+}\) density in the model compared to measurements may stem from the spacecraft orbiting along the edge of the larger \({{\rm{O}}}_{2}^{+}\) flux region, rendering the model flux sensitive to the exact location. Around 9:15, MAVEN observed a decrease in the proton and \({{\rm{O}}}_{2}^{+}\) densities. It entered the nightside and encountered an \({{\rm{O}}}_{2}^{+}\) density gap, as seen in the model (Extended Data Fig. 2j,k).

The comparison to MEX data is more difficult because of complications in the proton observations and the absence of magnetic field measurements. The flank shock was crossed at 08:20, which was marked by a significant increase in the electron energy spectrum (Extended Data Fig. 3b), although this effect was not mirrored in the proton density (Extended Data Fig. 3d) for the reasons outlined above. The modelled shock crossing was about 5 min late, possibly because the shock was highly dynamic, and therefore, the precise location may not match exactly. The modelled electron density agrees with the observations (Extended Data Fig. 3f). At 09:00, the proton fluxes vanished (Extended Data Fig. 3a), as MEX entered the proton void in agreement with the simulations (Extended Data Fig. 3j). The heavy ions became apparent (Extended Data Fig. 3c,e,k) even before the foreshock crossing at 07:50. The overall variability of heavy ions between observations and simulation (Extended Data Fig. 3e) aligns well, although the absolute values do not match perfectly. As it was difficult to reproduce all the details of the ionosphere in the model, we did not expect to achieve a quantity match between observations and models, instead we expected a quality match. The peak in the heavy-ion density (Extended Data Fig. 3e) at around 08:42, which is associated with the crossing of a tailward flow of heavy ions aligned with the local magnetic field, is well reproduced (Extended Data Fig. 3k). At 09:07, MEX entered the ionosphere, and cold ions became visible, as they did for MAVEN. From 09:15 onward, MEX was in the eclipse, as the photoelectron fluxes disappeared.